Rak =  rp + 2Rl
                      mu -1
substituting the variables,
       Rak =  280 + 2x300
                          2 -1
       Rak = 880.
    Here is an example of a cathode resistor so large in value that it must eliminated from the circuit or its large voltage drop must be included in a revaluation of the circuit variables. Since this SRPP must have a driver stage to make up for the low gain afforded by the 6AS7, at least one coupling capacitor will be needed. Therefore, the better solution is to use a fixed bias on the SRPP stage, as it eliminates the need for a cathode resistor and its bypass capacitor.
    The idle current can be found by using the following formula, now that we know the value of Rak:
      Iq = Vb / 4(rp + Rload + Rak),
substituting the variables,
      Iq = 200 / 4(280 + 300 + 880),
      Iq = 34 mA.
The idle current times Rak gives us the negative bias voltage needed:
      Vbias = IqRak,
      Vbias = 29.92 v.
    Now that we have taken care of the supporting details, let's see if our efforts were wasted. Once again we find the effective Gm of the top triode and take its inverse and then compare that value against Rak to see how well the formula worked.

Optimization and Gain

   gain =
                  muRL(rp + muRak + Ra)                .
(RL - muRak)RL - (RL+Rak+rp)(RL+Ra +rp)

New Variation
   In the last design example, the Iq was 34 mA. This amount of current was dictated by the formula for an optimized SRPP. What if we wish to run the tube at a lower idle current, say 30 or 20 mA? Then we must either use a lower power supply voltage or a higher load impedance, as the formula comprises these two variables. But what if we wish to retain both variables while running less current? Then a different circuit topology is needed.

   This variation takes the output at the midpoint of two resistors, R1 and R2, that replace the single resistor Rak. Since we have artificially decreased the idle current, we must artificially decrease the effective Gm of the top triode. Adding resistor R1 has the effect of increasing rp of the top triode to: 

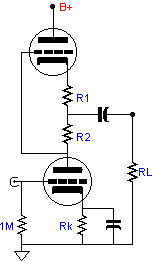
       rp´ = rp + (mu + 1)R1,
and since
      Gm = mu / rp,
the effective Gm becomes
      Gm´ = mu / [rp + (mu + 1)R1].
     Once again let's first set the load impedance to zero. Now the only load the bottom triode sees is resistor R2. Whatever signal voltage that develops across this resistor will be given to the top triode. The top triode must then match the bottom triode in increased and decreased current conduction to balance the push-pull operation. In other words, the inverse of the top triode's effective Gm must equal just the value of

Gm´=

                        mu

Ra + rp + [(mu + 1)Rak + rp][(Rak+rp)||Rl]
                                 rp + Rak

where Ra = Rak, thus       
     Gm´ = 0.001136 = 1.136 mA/v,
and
     880 = 1 / 0.001136.
And as Rak = 880, we know the formula also worked in this case.