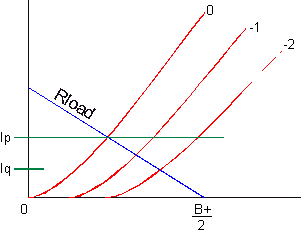
resistor, Rk: 
      Rak = Rk = ( Vb / 2Iq) - rp
                                  mu +1
The value of Rl seems to be missing from this equation, but it is implied in the calculation of the idle current Iq. But we could not find Iq until we found Rak. Reducing both formulae to one formula gives us our answer:
       Rak = Rk =  rp + 2Rl
                              mu -1
While this formula gains much by virtue of its simplicity, it hides from the tube circuit designer some key information, such as the value of the idle current, and by extension, the tube dissipation and the peak current into the load impedance. Still, it is intriguing to see Vb and Iq both drop out of the mix, which shows just how decisive the triode's mu and rp are in this circuit's functioning. This formula promises to give us the value of Rak that yields the biggest, cleanest voltage swing into the load resistance. Let's give it a test.
   If we set the load impedance to zero ohms, the formula reduces further to
     Rak = rp / (mu - 1),
which would yield 103 ohms as the correct value for a 6DJ8, as
     103 = 3300 / (33 - 1).
To verify this result, let's plug this value into the following formula:
     Gain = muR / (rp + R),
Which is the formula for the gain of a Grounded Cathode amplifier,
      Gain = 33 x 103 / (3300 + 103),
      0.9988 =  3399 / 3403.
The result easily rounds to 1, which means that a 1 volt pulse at the bottom tube's grid results in an increase in current draw sufficient to develop a -1 volt pulse at the top tube's grid.
    Substituting  200 ohms for the value of Rak shows an asymmetrical drive voltage:
      Gain = 33 x 200 / (3300 + 200),
      1.88 =  6600 / 3500, 
as does substituting 50 ohms for Rak:
      Gain = 33 x 50 / (3300 + 50),

  But how do we precisely determine the value of resistor Rak? Unfortunately, the simple rule that worked so well for MOSFETS, Rak = 1/Gm, will not work for triodes, as triodes have rp. Plate resistance is what separates triodes from FETs, MOSFETs, transistors, tetrodes, and pentodes. The rp is the resistance that a triode offers a small change in plate voltage. However, unlike the example of the MOSFET based SRPP circuit, the rp of top and bottom tubes greatly increase the complexity of the analysis of this circuit, as the circuit begins to resemble a knotty clump of rope: as we pull on one piece, some pieces bind together while others fall apart.
   Still, do not think of rp as a detriment, for without rp this circuit does not work very well. It is the rp of the triodes that gives the SRPP its low output impedance. The MOSFET-based SRPP circuit has wonderful current gain, but an unusable high output impedance; it is as if the pieces of rope were cut up into individual strands and left to float in a bowl, one piece can be moved without moving the others. Thus, finding the optimal value for Rak will require taking in account all the variables and interactions of the SRPP circuit.
  Here is the solution. Since we have split the B+ voltage equally between tubes and each tube sees an identical idle current, the value of Rak must equal the value of the cathode bias

<PREVIOUS

pg. 10

NEXT >