|
|
PSRR figure, as the rp of the triode defines the bottom element of a voltage divider, with the plate resistor defining the top element:
Ratio = rp / (rp + Ra).
On the other hand, the Cascode's high output impedance makes for a poor noise division:
Ratio = (mu + 2) rp / [(mu + 2) rp + Ra].
For example, a 6DJ8 used in a Grounded Cathode amplifier with a 9K plate load resistor and a bypassed cathode resistor, will allow only 25% of the noise at its power supply connection to make to its output, as its 3K rp defines only one quarter of the resistance presented to the power supply to ground:
Ratio = rp / (rp + Ra)
Ratio = 3,000 / (3000 + 9,000)
Ratio = 3,000 / 12,000
Ratio = 1 / 4 = .25.
When the 6DJ8 is used in a Cascode circuit, with the same 9K plate resistor, allows 92% of the noise at its power supply connection to make to its output; the math:
Ratio = (mu + 2) rp / [(mu + 2) rp + Ra]
Ratio = (33 +2) 3,000 / [(mu + 2) 3000 + 9,000]
Ratio = 105,000 / 114,000
Ratio = 1 / 1.086 = 0.92.
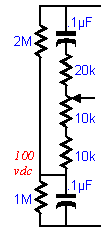
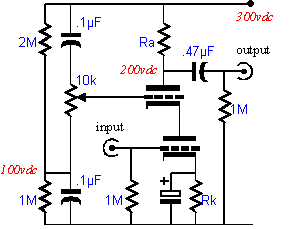
The Solution to a Poor PSRR
The Cascode circuit, when using triodes, has actually two inputs available. The first is the bottom triode's grid; the second, the top triode's grid. Normally, this second input is used only to connect to a fixed reference voltage, but it can also be used as a low-gain signal input. This is possible because of the triode's plate resistance. The rp of the bottom triode allows the bottom triode to function like the unbypassed cathode resistor in a Grounded Cathode amplifier. In other words, the top triode functions as a Grounded Cathode amplifier with its cathode in series with
|
|
|
|
|
the bottom triode's rp. The gain from the second input:
Gain = mu Ra / [ Ra + (mu + 1) Rk ].
For example, using a 6DJ8 with a plate resistor of 10K, the gain equals:
Gain = mu Ra / [ Ra + (mu + 1) rp ]
Gain = 33 10,000 / [ 10,000 + (33 + 1) 3,000 ]
Gain = 330,000 / [ 10,000 + 102,000 ]
Gain = 2.94.
Now this gain from the second input can be used to interject a sampling of the power supply noise, which will be in inverted phase at the output. If this inverted noise signal is equal in amplitude to the power supply noise, the two will null at the output. From the example above, the needed ratio of power supply noise is 1/2.94.
A Tweak
Now as tubes differ from each other and even differ from themselves over time, the best solution is not to hard-wire the ratio in place, but to use a potentiometer to allow a fine degree of noise nulling. The nulling can be adjusted for a signal stage or if the Cascode appears in a more complex circuit, to null the noise at the final output, as long as the phase shift between stages is nominal and the gain from the second input is sufficient to overwhelm the noise added from the other stages.
A Further Tweak
|
|
|