A Series-Shunt Regulator
   Combining the series and the shunt regulator might prove the best compromise. The benefits from each type can be added together in one regulator. The series regulator half provides the compliant current sourcing that improves the efficiency and PSRR of the regulator and the shunt half of regulator provides the net current canceling function to keep load's current swings contained to the regulator. Putting both regulator together requires only a little imagination, as the regulator will look and function much like a totem pole push-pull amplifier.

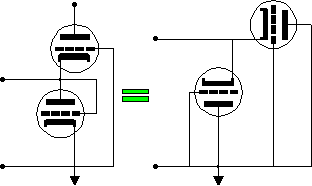
     IΔ = (1 + mu) / rp,
Which equals the absolute decrease in current the top triode experiences:
     IΔ = -1 / rp  +  -1 x Gm
     IΔ = -1 / rp  +  -mu / rp
     IΔ = -(1 + mu) / rp.
In other words, 100% feedback from plate to grind in a grounded cathode amplifier make this amplifier function identically to a cathode follower, which also experiences 100%  degenerative feedback.

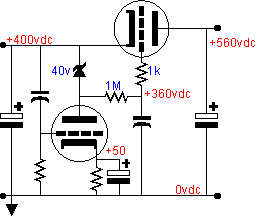
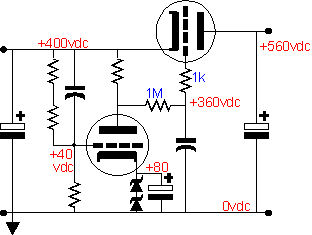
   Adding DC sensitivity to the regulator can accomplished by working on the top or the bottom triode's grid, but not both. Asides from extra complexity, it is not a good idea to have an internecine battle between both triodes over small reference voltage differences. The circuit below is one example of how DC correction could be added to the regulator (note the replacement of the zener by the plate resistor).
                                  //JRB

    The regulator shown above relies on both tubes to counter any perturbations at the output of the regulator. The top tube functions as a cathode follower whose grid is AC grounded; the bottom tube functions as a grounded cathode amplifier with 100% feedback from the plate being applied to its grid. In effect what is created is two cathode followers, as the feedback given to the bottom tube yields the same performance as the top tube achieves as a cathode follower. Put analytically, a 1 volt pulse applied to the bottom triode's plate will be met with an increase in current flow through the triode equal to the 1 volt divided by the rp of the triode plus the transconductance of the triode times the 1 volt, which can be expressed as
    IΔ = 1 / rp  +  1 x Gm
    IΔ = 1 / rp  +  mu / rp